高斯函数的方差

$$
\operatorname{var}(x)=E\left(x^2\right)-E[x]^2=\sigma^2
$$

证明

我们已知高斯函数的期望为$E(x)=\mu$,然后通过方差的定义可以得到$var(x)=E[(x-u)^2]$所以我们可以得到
$$
\operatorname{Var}(X)=\mathbb{E}\left[(X-\mu)^2\right]=\int_{-\infty}^{\infty}(x-\mu)^2 f(x) d x
$$
最终的表达式如下:
$$
\operatorname{Var}(X)=\int_{-\infty}^{\infty}(x-\mu)^2 \frac{1}{\sqrt{2 \pi \sigma^2}} \exp \left(-\frac{(x-\mu)^2}{2 \sigma^2}\right) d x
$$

变量替换

然后我们令$z=x-\mu$且$\frac{1}{\sqrt{2\pi\sigma^{2}}}$为常数项所以
$$
\begin{array}{r}{\mathrm{Var}(X)=\frac{1}{\sqrt{2\pi\sigma^{2}}}\int_{-\infty}^{\infty}z^{2}\exp\left(-\frac{z^{2}}{2\sigma^{2}}\right),d z}\end{array}
$$
所以我们最后相当于要计算的就是
$$
I-\int_{-\infty}^{\infty}z^{2}\exp\left(-\frac{z^{2}}{2\sigma^{2}}\right)~{}d z
$$
我们通过分布积分来优化一下这个函数
$$
\begin{array}{r}{\int\dot{u},d\nu=\dot{u}\mathrm{v}-\int\dot{u}\dot{d u}.}\end{array}
$$
令$u=z$,$dv=z\exp\left(-\frac{z^{2}}{2\sigma^{2}}\right)\ d z$
则有$du=dz$,$\int dv=\int z\exp\left(-\frac{z^{2}}{2\sigma^{2}}\right)\ d z$
然后v和z的关系式可以这样去求
令$u=\frac{z^{2}}{2\sigma^{2}}$则$d u=\frac{z}{\sigma^{2}}d_{2}$
带入积分公式后可得
$$
v(z)=\int\exp(-u)\cdot\sigma^{2},d u
$$
最终可以得到表达式
$$
v(z)=-\sigma^{2}\exp\left(-\frac{z^{2}}{2\sigma^{2}}\right)+C
$$
已知令$u=z$和$v(z)=-\sigma^{2}\exp\left(-\frac{z^{2}}{2\sigma^{2}}\right)+C$

分布积分

运用分布积分我们可以得到

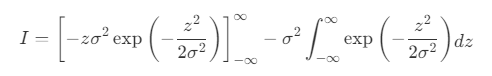
首先是第一项:$\begin{array}{r}{\left[-z\sigma^{2}\exp\left(-\frac{z^{2}}{2\sigma^{2}}\right)\right]_{-\infty}^{\infty}}\end{array}$

满足$f(x)=-f(-x)$所以为奇函数，所以他的积分为0
然后看第二项:

$$
\sigma^{2}\int_{-\infty}^{\infty}\exp\left(-\frac{z^{2}}{2\sigma^{2}}\right)\ dz
$$

我们从《高斯函数的期望》可以得到

$$
I=\int_{-\infty}^{\infty}\exp\left(-\frac{x^{2}}{2}\right)\ d x
$$

$$
I=\sqrt{2\pi}
$$

所以第二项的结果为:$I=\sigma^{2}\cdot\sqrt{2\pi\sigma^{2}}$
所以高斯函数的方差是:

$$
\mathrm{Var}(X)=\frac{1}{\sqrt{2\pi\sigma^{2}}}\cdot I=\frac{1}{\sqrt{2\pi\sigma^{2}}}\cdot\sigma^{2}\cdot\sqrt{2\pi\sigma^{2}}=\sigma^{2}
$$