线性代数是研究有限维向量空间上的线性映射的学问
集合 $R^2$(你可以将其视作一个平面)是全体有序实数对所构成的集合:
$$R^2 = {(𝑥, 𝑦) : 𝑥, 𝑦 ∈ R}.$$
集合 $R3$(你可以将其视作通常的三维空间)是全体有序实数三元组所构成的集合:
$$R^3 = {(𝑥, 𝑦, 𝑧) : 𝑥, 𝑦, 𝑧 ∈ R}.$$
$F^𝑛$ 是全体具有 𝑛 个 F 中元素的组所构成的集合:
$$
F^𝑛 = {(𝑥^1, . . . , 𝑥^𝑛) : 对于 𝑘 = 1, . . . , 𝑛 有 𝑥^𝑘 ∈ F}.\
对于 (𝑥^1, . . . , 𝑥^𝑛) ∈ F
𝑛 和 𝑘 ∈ {1, . . . , 𝑛},\
我们称 𝑥^𝑘 是 (𝑥^1, . . . , 𝑥^𝑛) 的第 𝑘 个坐标.
$$

一个域是这样一种集合:它包含至少两个不同的元素(称作 0 和 1),R 和 C 都是域,定义了通常的加法和乘法运算的有理数集合也是域.域的另一个例子是集合 {0, 1},它具有通常的加法和乘法运算,除了 1 + 1 被定义为等于 0.
向量空间
一个向量空间是一个集合 $𝑉$,$𝑉$上的加法和标量乘法满足下列性质:
可交换性(commutativity)
$$
对于所有 𝑢, 𝑣 ∈ 𝑉,都有 𝑢 + 𝑣 = 𝑣 + 𝑢.
$$
可结合性(associativity)
$$
对于所有 𝑢, 𝑣, 𝑤 ∈ 𝑉 以及所有 𝑎, 𝑏 ∈ F,都有 (𝑢 + 𝑣) + 𝑤 = 𝑢 + (𝑣 + 𝑤) 以及 (𝑎𝑏)𝑣 =
𝑎(𝑏𝑣).
$$
加法恒等元(additive identity)
$$
对于所有 𝑣 ∈ 𝑉,都存在 0 ∈ 𝑉 使得 𝑣 + 0 = 𝑣.$$
加法逆元(additive inverse)
$$
对于每个 𝑣 ∈ 𝑉,都存在 𝑤 ∈ 𝑉 使得 𝑣 + 𝑤 = 0.
$$
乘法恒等元(multiplicative identity)
$$
对于所有 𝑣 ∈ 𝑉,都有 1𝑣 = 𝑣.
$$
分配性质(distributive properties)
$$
对于所有 𝑢, 𝑣 ∈ 𝑉 以及所有 𝑎, 𝑏 ∈ F,都有 𝑎(𝑢 + 𝑣) = 𝑎𝑢 + 𝑎𝑣 且 (𝑎 + 𝑏)𝑣 = 𝑎𝑣 + 𝑏𝑣.
$$
向量空间的元素被称作向量或点.
$F^S$的定义(和开头序列的定义要对应起来比较好理解)
- 如果 $𝑆$是一个集合,那么 $F^𝑆$ 表示从 $𝑆$ 到 $F$ 的所有函数构成的集合.
- 对于 $𝑓 , 𝑔 ∈ F^𝑆$,和 $𝑓 + 𝑔 ∈ F^𝑆$是由下式定义的函数:对于所有 $𝑥 ∈ 𝑆$,
$$
( 𝑓 + 𝑔) (𝑥) = 𝑓 (𝑥) + 𝑔(𝑥).
$$ - 对于 $𝜆 ∈ F 与 𝑓 ∈ F^𝑆$,乘积 $𝜆 𝑓 ∈ F^𝑆$ 是由下式定义的函数:对于所有 $𝑥 ∈ 𝑆$,
$$
(𝜆 𝑓 ) (𝑥) = 𝜆 𝑓 (𝑥).
$$
S可以理解为定义域,F理解为值域,换句话说,
$𝐹^𝑆$ 中的每一个元素都是一个函数,它把集合
$𝑆$ 中的每一个元素映射到集合 $𝐹$ 中的某个元素。
向量空间 $F^𝑛$是向量空间 $F^𝑆$的一个特例,因为每个 $(𝑥^1, . . . , 𝑥^𝑛) ∈ F^𝑛$都可被视作一个从集合 {1, 2, . . . , 𝑛} 到 $F$ 的函数 $𝑥$,只要将$(𝑥^1, . . . , 𝑥^𝑛)$ 的第 $𝑘$ 个坐标写成 $𝑥(𝑘)$ 而不是 $𝑥_k$.
加法逆元唯一:向量空间里的每个元素都有唯一的加法逆元.
证明 设$𝑉$是向量空间.令 $𝑣 ∈ 𝑉$.假设 $𝑤 $和 $𝑤^′$ 都是 $𝑣$ 的加法逆元.那么
$$
𝑤 = 𝑤 + 0 = 𝑤 + (𝑣 + 𝑤^′) = (𝑤 + 𝑣) + 𝑤^′ = 0 + 𝑤^′ = 𝑤^′
$$
由此 $𝑤 = 𝑤^′$,命题得证.



子空间
如果 𝑉 的子集 𝑈 是与 𝑉 具有相同的加法恒等元、加法和标量乘法运算的向量空间,那么 𝑈 就称为 𝑉 的子空间.
当且仅当 𝑉 的子集 𝑈 满足以下三个条件时,𝑈 是 𝑉 的子空间.
加法恒等元
$$0 ∈ 𝑈.$$
对于加法封闭
$$𝑢, 𝑤 ∈ 𝑈 意味着 𝑢 + 𝑤 ∈ 𝑈.$$
对于标量乘法封闭
$$𝑎 ∈ F 且 𝑢 ∈ 𝑈 意味着 𝑎𝑢 ∈ 𝑈.$$
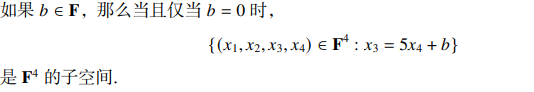




齐次线性方程的解集是一个子空间,且要满足零解的问题。





对于1.来说因为f(x)=0为一个常数所以他的导数为0


子空间的和
假设 $𝑉^1, . . . , 𝑉^𝑚$ 是 𝑉 的子空间.$𝑉^1, . . . , 𝑉^𝑚$ 的和是由 $𝑉^1, . . . , 𝑉^𝑚$ 中元素所有可能的和所构成的集合,记作$𝑉^1 + · · · + 𝑉^𝑚$.更确切地说,
$$𝑉^1 + · · · + 𝑉^𝑚 = {𝑣^1 + · · · + 𝑣^𝑚 : 𝑣^1 ∈ 𝑉^1, . . . , 𝑣^𝑚 ∈ 𝑉^𝑚}.$$

子空间的和是包含这些子空间的最小子空间
假设 $𝑉_1, . . . , 𝑉_𝑚$是 𝑉 的子间,那么$𝑉_1 + · · · + 𝑉_𝑚$ 是最小的包含 $𝑉_1, . . . , 𝑉_𝑚$ 的子空间.
直和:
设 $𝑉_1, . . . , 𝑉_𝑚$ 是 𝑉 的子空间.$𝑉_1 + · · · + 𝑉_𝑚$的每个元素都可以被写成这种形式
$𝑣_1 + · · · + 𝑣_𝑚$,
其中每个 $𝑣_𝑘 ∈ 𝑉_𝑘$.我们特别感兴趣的是 $𝑉_1 + · · · +𝑉_𝑚$ 中的每个向量都能唯一地用上述形式表示
的情况.这种情况十分重要,所以它获得了专属的名称(直和)以及专属的符号(⊕).
设 $𝑉_1, . . . , 𝑉_𝑚$ 是 𝑉 的子空间.
- 如果 $𝑉_1, . . . , 𝑉_𝑚$ 中的每个元素都能用 $𝑣_1 + · · · + 𝑣_𝑚$(其中各 $𝑣𝑘 ∈ 𝑉𝑘$)这种形式唯一
- 地表示出来,则称子空间之和 $𝑉_1, . . . , 𝑉_𝑚$ 为直和.
如果$𝑉_1, . . . , 𝑉_𝑚$是直和,那么用 𝑉1 ⊕ · · · ⊕ 𝑉𝑚 来表示$𝑉_1, . . . , 𝑉_𝑚$,其中记号 ⊕ 表示
此处的和是直和.
** 零属于公共向量 **
直和的条件:假定$𝑉_1, . . . , 𝑉_𝑚$是 𝑉 的子空间.那么$𝑉_1, . . . , 𝑉_𝑚$ 是直和,当且仅当用 $𝑣_1 + · · · + 𝑣_𝑚$(其中各 𝑣𝑘 ∈ 𝑉𝑘)表示 0 的唯一方式是将每个 𝑣𝑘 都取 0.
两个子空间的直和:
假定 𝑈 和 𝑊 是 𝑉 的子空间.那么𝑈 + 𝑊 是直和 ⇐⇒ 𝑈 ∩ 𝑊 = {0}
习题