分布变化
VAE和GAN的本质都是希望重构一个隐变量$Z$生成目标数据$X$,换一种方式来说就是假设$Z$符合某些分布,然后训练一个模型$X=g(Z)$将概率分布映射到X就是从结果映射回训练集(个人理解)
VAE主要就是为了解决下面这个问题
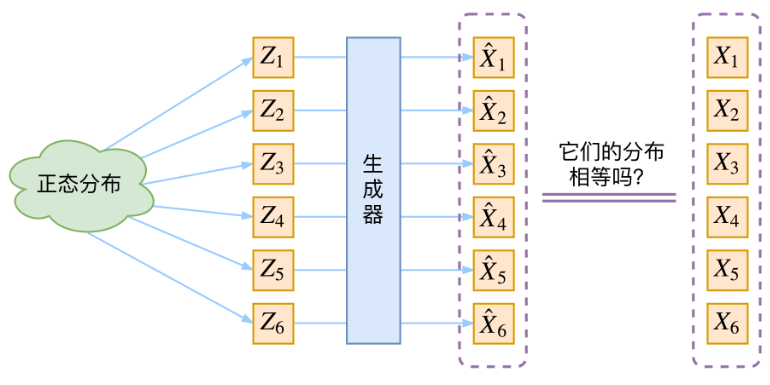
VAE理解误区
那现在假设$Z$服从标准的正态分布,那么我就可以从中采样得到若干个$Z1,Z2,…,Zn$,然后对它做变换得到$X^1=g(Z1),X^2=g(Z2),…,X^n=g(Zn)$,我们怎么判断这个通过$g$构造出来的数据集,它的分布跟我们目标的数据集分布是不是一样的呢?有读者说不是有KL散度吗?当然不行,因为KL散度是根据两个概率分布的表达式来算它们的相似度的,然而目前我们并不知道它们的概率分布的表达式,我们只有样本本身而没有分布表达式就没办法计算KL散度。
首先我们有一批数据样本${X1,…,Xn}$其整体用$X$描述,我们本想根据${X1,…,Xn}$到$X$布$p(X)$如果能得到的话,那我直接根据$p(X)$采样,就可以得到所有可能的$X$(包括${X1,…,Xn}$外的),这是一个终极理想的生成模型了。当然,这个理想很难实现,于是我们将分布改一改
$$
p(X)=\sum_Z p(X \mid Z) p(Z)
$$
$p(X|Z)$就描述了一个由$Z$来生成$X$的模型,而我们假设$Z$服从标准正态分布,$p(Z)=N(0,I)$。如果这个理想能实现,那么我们就可以先从标准正态分布中采样一个$Z$,然后根据$Z$来算一个$X$,也是一个很棒的生成模型。接下来就是结合自编码器来实现重构,保证有效信息没有丢失,再加上一系列的推导,最后把模型实现。框架的示意图如下:
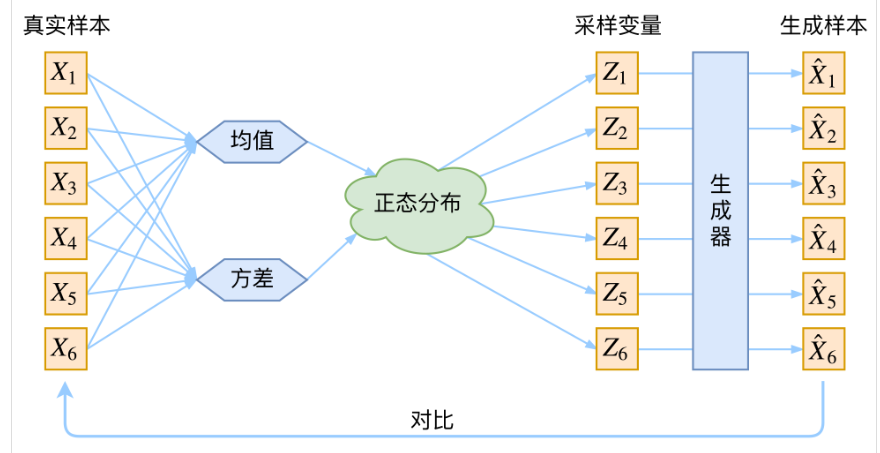
如果按照上述流程的话会出现一个问题,无法保证重新采样出来的$Z_k$是否还对应着远来的$X_k$,。
一致性
在VAE中没有假设$p(Z)$是符合正太分布的,假设的是$p(Z|X)$是符合正太分布的。
给定一个真实样本$X_k$,我们假设存在一个专属于$X_k$的分布$p(Z|Xk)$,并进一步假设这个分布是(独立的、多元的)正态分布。为什么要强调“专属”呢?因为我们后面要训练一个生成器$X=g(Z)$,希望能够把从分布$P(Z|X_k)$采样出来的一个$Z_k$还原为$X_k$。如果假设$p(Z)$是正态分布,然后从$p(Z)$中采样一个$Z$,那么我们怎么知道这个$Z$对应于哪个真实的$X$呢?现在$p(Z|X_k)$专属于$X_k$,我们有理由说从这个分布采样出来的$Z$应该要还原到$X_k$中去。
此时每一个$X_k$都有一个专属的正太分布方便后面的生成器进行还原,正太分布有两个参数均值 $\mu$ 和方差 $\sigma^2$,此时我们采用神经网络来拟合他们正太分布的均值和方差,具体流程如下:
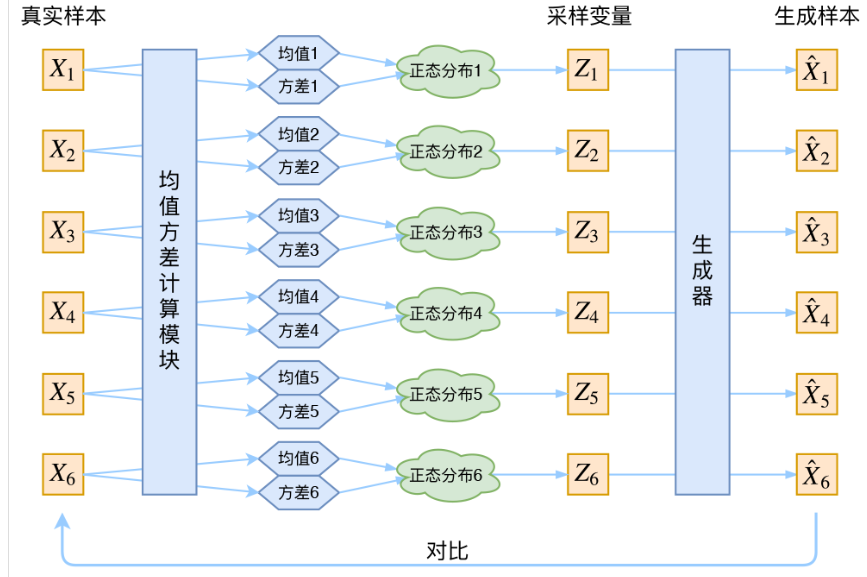
随机性
首先,我们希望重构$X$,也就是最小化$D(X^k,X_k)^2$,但是这个重构过程受到噪声的影响,因为$Z_k$是通过重新采样过的,不是直接由encoder算出来的。显然噪声会增加重构的难度,不过好在这个噪声强度(也就是方差)通过一个神经网络算出来的,所以最终模型为了重构得更好,肯定会想尽办法让方差为0。而方差为0的话,也就没有随机性了,所以不管怎么采样其实都只是得到确定的结果(也就是均值),只拟合一个当然比拟合多个要容易,而均值是通过另外一个神经网络算出来的。
说白了,模型会慢慢退化成普通的AutoEncoder,噪声不再起作用。
这样不就白费力气了吗?说好的生成模型呢?
别急别急,其实VAE还让所有的$p(Z|X)$都向标准正态分布看齐,这样就防止了噪声为零,同时保证了模型具有生成能力。怎么理解“保证了生成能力”呢?如果所有的$p(Z|X)$都很接近标准正态分布$N(0,I)$,那么根据定义
$$
p(Z)=\sum_X p(Z \mid X) p(X)=\sum_X \mathcal{N}(0, I) p(X)=\mathcal{N}(0, I) \sum_X p(X)=\mathcal{N}(0, I)
$$
这样我们就能达到我们的先验假设:$p(Z)$是标准正态分布。然后我们就可以放心地从$N(0,I)$中采样来生成图像了.