IOU和他们儿子们

IOU

$IOU$又名交并比，简单来说就是你网络给出的预测框与真实框的一个交集。

如上图所示，红色部分是我们的真实框也就是标注数据集的时候你自己画出来的，而绿的框则是网络预测出来的。他们之间的交集除以他们的并集就是$IOU$。
这里给出$IOU$的定义:
$$
IOU=\frac {|A\cap B |}{|A\cup B |}
$$
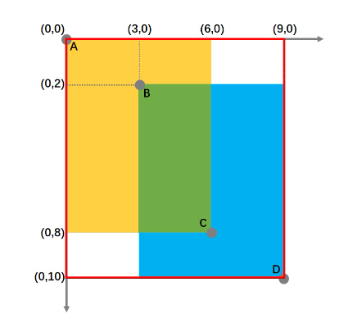
这里给出一个别人已经画好的图

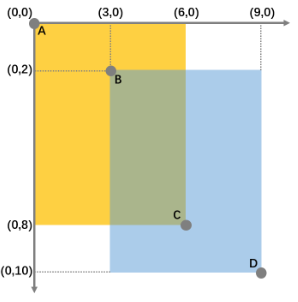
对于这张图来说$IOU$要如何计算呢
$$
IOU=\frac {绿色}{黄色+蓝色-绿色}\
=\frac{(C_x-B_x)·(C_y-B_y)}{(C_x-A_x)·(C_y-A_y)+(D_x-B_x)·(D_y-D_y)-(C_x-B_x)·(C_y-B_y)}
$$
接下来给出代码实现

def IoU(box1, box2):
    #这里的box是xyxy形式的
    # 计算中间矩形的宽高
    in_h = min(box1[2], box2[2]) - max(box1[0], box2[0])
    in_w = min(box1[3], box2[3]) - max(box1[1], box2[1])
    
    # 计算交集、并集面积
    inter = 0 if in_h < 0 or in_w < 0 else in_h * in_w
    union = (box1[2] - box1[0]) * (box1[3] - box1[1]) + \
            (box2[2] - box2[0]) * (box2[3] - box2[1]) - inter
    # 计算IoU
    iou = inter / union
    return iou

$IOU$的两个缺点：
(1).当预测框和真实框的不存在交集的时候，如下图所示.如何使用$IOU$进行计算的话，其定位损失就为0，导致梯度为0无法进行优化。

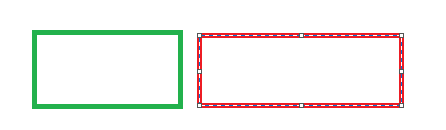
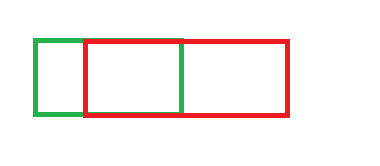
(2).IoU无法精确的反映两者的重合度大小。如下图所示，三种情况IoU都相等，但看得出来他们的重合度是不一样的，左边的图回归的效果最好，右边的最差。

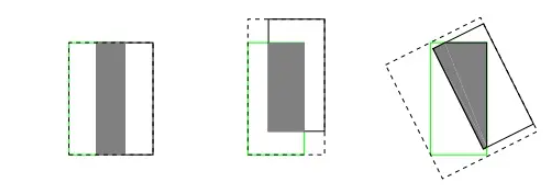
GIOU

$GIOU$的提出解决了$IOU$的第一个缺点，给出$GIOU$的定义
$$
GIOU=IOU-\frac {C-|A\cap B |}{C}
$$
$C$为这两个框的最小外接矩形
下面还用刚刚那个例子来进行计算

$$
GIOU=IOU-\frac {红框-(黄色+蓝色-绿色)}{红框}
$$
给出$GIOU$的代码

def GIoU(box1, box2):
    # 计算最小包庇面积
    y1,x1,y2,x2 = box1 
    y3,x3,y4,x4 = box2
    area_C = (max(x1,x2,x3,x4)-min(x1,x2,x3,x4)) * \
             (max(y1,y2,y3,y4)-min(y1,y2,y3,y4))
    
    # 计算IoU
    in_h = min(box1[2], box2[2]) - max(box1[0], box2[0])
    in_w = min(box1[3], box2[3]) - max(box1[1], box2[1])
    inter = 0 if in_h < 0 or in_w < 0 else in_h * in_w
    union = (box1[2] - box1[0]) * (box1[3] - box1[1]) + \
            (box2[2] - box2[0]) * (box2[3] - box2[1]) - inter
    iou = inter / union
    
    # 计算空白部分占比
    end_area = (area_C - union)/area_C
    giou = iou - end_area
    return giou

$GIOU$的缺点：当两个框处于下图状态的时候$GIOU$就退化成了$IOU$。

DIOU

$DIOU$在$GIOU$加上了预测框与真实框之间的距离，给出他的定义：
$$
DIOU=IOU-\frac {ρ^2·(b,b^gt)}{c^2}
$$
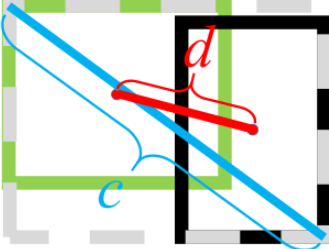
其中$b$，$b^gt$分别代表两个框的中心点，$ρ$代表两个中心点之间的欧氏距离，$C$代表最小包庇矩形的对角线，即如下图所示：

$DIOU$实现的代码

def DIoU(box1, box2):
    # 计算对角线长度
    y1,x1,y2,x2 = box1 
    y3,x3,y4,x4 = box2
    C = np.sqrt((max(x1,x2,x3,x4)-min(x1,x2,x3,x4))**2 + \
                (max(y1,y2,y3,y4)-min(y1,y2,y3,y4))**2)
    
    # 计算中心点间距
    point_1 = ((x2+x1)/2, (y2+y1)/2)
    point_2 = ((x4+x3)/2, (y4+y3)/2)
    D = np.sqrt((point_2[0]-point_1[0])**2 + \
                (point_2[1]-point_1[1])**2)

    # 计算IoU
    iou = IoU(box1, box2)

    # 计算空白部分占比
    lens = D**2 / C**2
    diou = iou - lens
    return diou

CIOU

在$GIOU$的基础之上加入了形状的相似度：
$$
CIOU=IOU-\frac {ρ^2·(b,b^gt)}{c^2}-\alpha\upsilon
$$
其中$\alpha$是权重函数，而$\upsilon$用来度量长宽比的相似性：
$$
\upsilon= \frac{4}{\pi^{2}} *\left(\arctan \frac{w^{g t}}{h^{g t}}-\arctan \frac{w}{h}\right)^2
$$
$$
\alpha= \frac{\upsilon}{(1-IOU)+\upsilon}
$$
在使用$CIOU$作为Loss的时候，$\upsilon$的梯度同样会参与反向传播的计算，其中：
$$
\begin{aligned}
\frac{\partial v}{\partial w} & =2 * \frac{4}{\pi^{2}} *\left(\arctan \frac{w^{g t}}{h^{g t}}-\arctan \frac{w}{h}\right) *(-1) * \frac{1}{1+\left(\frac{w}{h}\right)^{2}} * \frac{1}{h} \
& =\frac{8}{\pi^{2}} *\left(\arctan \frac{w^{g t}}{h^{g t}}-\arctan \frac{w}{h}\right) *(-1) * \frac{h^{2}}{w^{2}+h^{2}} * \frac{1}{h} \
& =-\frac{8}{\pi^{2}} *\left(\arctan \frac{w^{g t}}{h^{g t}}-\arctan \frac{w}{h}\right) * \frac{h}{w^{2}+h^{2}}
\end{aligned}
$$
$$
\begin{aligned}
\frac{\partial v}{\partial h} & =2 * \frac{4}{\pi^{2}} *\left(\arctan \frac{w^{g t}}{h^{g t}}-\arctan \frac{w}{h}\right) *(-1) * \frac{1}{1+\left(\frac{w}{h}\right)^{2}} * w *(-1) * h^{-2} \
& =\frac{8}{\pi^{2}} *\left(\arctan \frac{w^{g t}}{h^{g t}}-\arctan \frac{w}{h}\right) * \frac{h^{2}}{w^{2}+h^{2}} * w * h^{-2} \
& =\frac{8}{\pi^{2}} *\left(\arctan \frac{w^{g t}}{h^{g t}}-\arctan \frac{w}{h}\right) * \frac{w}{w^{2}+h^{2}}
\end{aligned}
$$

def CIoU(box1, box2):
    y1,x1,y2,x2 = box1 
    y3,x3,y4,x4 = box2
    
    iou = IoU(box1, box2)
    diou = DIoU(box1, box2)

    v = 4 / math.pi**2 * (math.atan((x2-x1)/(y2-y1)) - \
                          math.atan((x4-x3)/(y4-y3)))**2 + 1e-5
    alpha = v / ((1-iou) + v)
    
    ciou = diou - alpha * v
    return ciou
CIoU(box1, box2)