1信息量
一件事情发生的概率越大信息量就会越少,举个例子国足每年都踢不进世界杯,这件事发生概率极大,大家都习以为常,但是假如有一年国足踢进的话,那这信息量就很大了,因为事情发生的概率极小。
若事件$x$发生的概率为$P(x)$,则信息量的计算公式为:
$$
I(x)=-\log(P(x))
$$
$\log$的底你可以随意取,但是在神经网络一般取e,这里拿一张别人的图
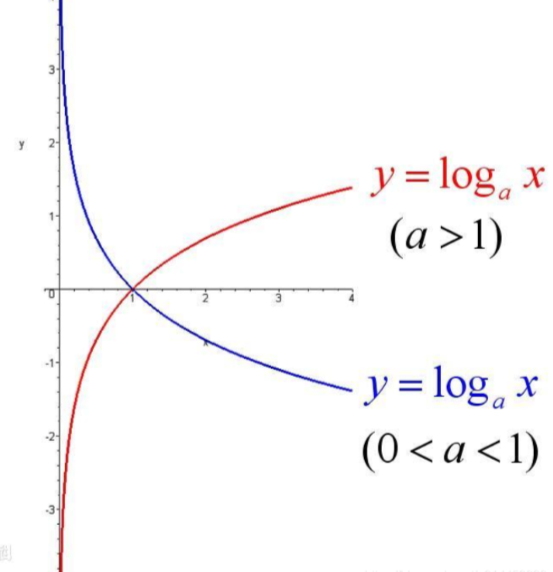
由图我们可以看出当log的底大于1,log的图形就像下图红色线,因为$P(x)$为概率的取值范围是$[0-1]$从图像可以看出满足我们上述对信息量的要求。
2信息熵
信息熵也被称为熵,用来表示所有信息量的期望,期望是试验中每次可能结果的概率乘以其结果的总和。
$$
H(x)=-\sum_{i=1}^{n} P(x_{i})·\log(P(x_i))
$$
3KL散度(相对熵)
机器学习中,常常用$P(x)$表示样本的真实分布,用$Q(x)$表示模型预测的分布,比如在一个五分类任务中(猫狗马鸟人分类器),$[x1,x2,x3,x4,x5]$分别表示猫狗马鸟人的概率,此时输入一张狗的照片其真实分布为$P(x)=[0,0,0,0,1]$那么$P(x)$和$Q(x)$就是两个不同的概率分布,可以用KL散度来计算他们的差异:
$$
D_{K L}(p | q)=\sum_{i=1}^{N}\left[p\left(x_{i}\right) \log p\left(x_{i}\right)-p\left(x_{i}\right) \log q\left(x_{i}\right)\right]
$$
怎么将KL散度转换到交叉熵呢,首先我们变形一下
$$
D_{K L}(p | q)=\sum_{i=1}^{N}\left[p\left(x_{i}\right) \log p\left(x_{i}\right)-p\left(x_{i}\right) \log q\left(x_{i}\right)\right]
\=-\sum_{i=1}^{N}p(x_i)\log(q(x_i))-H(p(x))
$$
由上式我们可以得到KL散度=交叉熵-信息熵
交叉熵是用来衡量两个概率分布的距离(也可以叫差别)。概率分布:即$[0.1,0.5,0.2,0.1,0.1]$,每个类别的概率都在$0~1$,且加起来为$1$。交叉熵的公式为:
$$
H(p,q)=-\sum_{i=1}^{N}p(x_i)\log(q(x_i))
$$